Jak przekonwertować pomiędzy systemami dziesiętnym i dziesiętnym?
Zanim przejdziemy do rozmowy na temat konwersji jednego systemu numerycznego na drugi, porozmawiajmy trochę o samym systemie numerycznym. System liczbowy można zdefiniować jako zestaw różnych kombinacji symboli, przy czym każdy z nich ma określoną wagę. Każdy system liczbowy jest różnicowany na podstawie radixa lub podstawy, na której system liczbowy jest tworzony. Radiks lub podstawa definiuje całkowity brak różnych symboli, który jest używany w danym systemie liczbowym. Na przykład, radix w systemie liczb binarnych wynosi 2, radix w systemie liczb dziesiętnych wynosi 10, a radix w systemie liczb ósemkowych wynosi 8.
System numeracji oktanowej:
Jak sama nazwa wyraźnie wskazuje, ten system liczbowy oparty jest na radiksie równym 8. Tak więc, w tym systemie liczbowym mamy osiem różnych cyfr. Dla ułatwienia uważamy te osiem cyfr za takie same jak pierwsze osiem cyfr w systemie dziesiętnym. Położenie każdej cyfry ósemkowej jest związane z pewną potęgą 8 i ta potęga równa jest indeksowi cyfry z lewej strony. Maksymalnie trzy cyfry binarne reprezentują jedną liczbę ósemkową w postaci binarnej. Ponieważ podstawą tego systemu liczbowego jest pewna potęga dwóch, bardzo łatwo i wygodnie jest zamienić liczbę ósemkową w system liczb binarnych lub szesnastkowych, które są używane w komputerach do wykonania całej pracy.
Liczby oktawowe nie znajdują bezpośredniego zastosowania w maszynach komputerowych, ponieważ komputery pracują na stanach binarnych lub bitach. Ponieważ jednak liczba ósemkowa zajmuje mniej cyfr, które mają być reprezentowane w układzie binarnym, mogą one być efektywnie przechowywane w komputerze bez marnowania miejsca w pamięci, jak np. liczba BCD(Binary Coded Decimal).
Konwersja systemu liczb dziesiętnych na dziesiętne:
Konwersja liczb dziesiętnych na ośmiokrotne jest bardzo podobna do konwersji liczb dziesiętnych na binarne. Jedyną różnicą jest to, że tym razem liczbę dziesiętną podzielimy na 8 zamiast na 2. Konwersję można wykonać wykonując poniższe czynności pisemne:
- Krok 1: Podziel liczbę dziesiętną przez 8, zanotuj resztę i przypisz do niej wartość R1. Podobnie, zanotuj iloraz i przypisz do niego wartość Q1.
- Krok 2: Teraz podziel Q1 z 8, zanotuj resztę i iloraz. Przypisz wartość R2 i Q2 do reszty i ilorazu uzyskanego w tym kroku.
- Krok 3: Powtarzaj sekwencję do momentu uzyskania wartości ilorazu (Qn) równego 0.
- Krok 4: Liczba ósemkowa będzie wyglądać tak.: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Przykład: Weźmy pod uwagę liczbę dziesiętną 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Więc, ekwiwalent OCTAL z 2181 jest:
(2181) Decimal = (4205) Octal
Konwersja ośmiokąta na system liczb binarnych:
Ponownie, konwersja liczby ósemkowej na dziesiętną jest bardzo podobna do konwersji liczby binarnej na dziesiętną, z tą tylko różnicą, że tym razem będziemy mnożyć cyfry z mocą 8 zamiast 2. Przeliczenia można dokonać wykonując poniższe czynności pisemne:
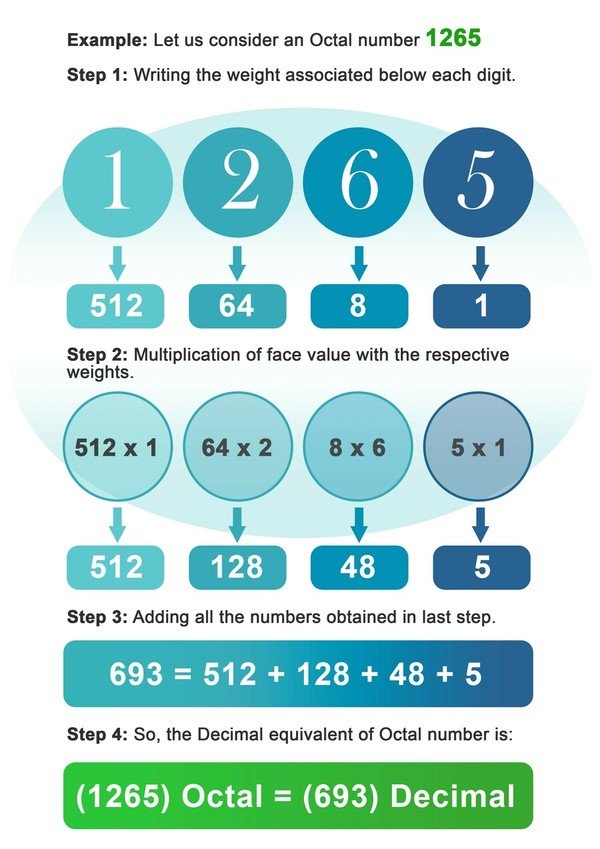
- Etap 1: Zapisać wagę 8 przypisaną poniżej każdej cyfry liczby ósemkowej.
- Krok 2: Teraz pomnóż każdą cyfrę przez wagę przypisaną do tego miejsca lub indeksu cyfry.
- Krok 3: Dodaj wszystkie liczby otrzymane po pomnożeniu w poprzednim kroku.
- Etap 4: Liczba uzyskana w ostatnim etapie jest dziesiętnym odpowiednikiem liczby ósemkowej.
Przykład: Rozważmy liczbę oktalową 1265.