Como converter entre os sistemas de números Octal e Decimal?
Antes de entrarmos na conversa de conversão de um sistema numérico em outro, vamos falar um pouco sobre o próprio Sistema Numérico. O Sistema Numérico pode ser definido como o conjunto das diferentes combinações de símbolos, com cada símbolo com um peso específico. Qualquer Sistema de Números é diferenciado com base no radix ou na base sobre a qual o sistema de números é feito. O Radix ou a Base define o número total de símbolos diferentes, que é usado em um determinado sistema de numeração. Por exemplo, o radix do sistema de número binário é 2, o radix do sistema de número decimal é 10, e o radix do sistema de número octal é 8.
O Sistema de Números Octal:
Como o nome claramente significa, este sistema de números é baseado em radix igual a 8. Portanto, neste sistema de números temos oito dígitos distintos. Para facilitar, consideramos estes oito dígitos como os primeiros oito dígitos no sistema numérico decimal. A posição de cada dígito octal está associada a alguma potência de 8 e esta potência é igual ao índice do dígito a partir da posição esquerda. São necessários no máximo três dígitos binários para representar um dígito octal na forma binária. Como a base deste sistema numérico em si é alguma potência de dois, é muito fácil e conveniente interconverter o número octal em sistema numérico binário ou hexadecimal que são usados em computadores para fazer todo o trabalho.
Os números de octal não encontram aplicação directa na maquinaria informática porque os computadores funcionam em estados ou bits binários. No entanto, como o número octal ocupa menos dígitos para ser representado em binário, eles podem ser eficientemente armazenados no computador sem qualquer desperdício de espaço na memória como o número BCD(Binary Coded Decimal).
Conversão de Decimal para Octal Number System:
A conversão do decimal para octal é muito semelhante à conversão do decimal em binário. A única diferença é que, desta vez, vamos dividir o número decimal com 8 em vez de 2. A conversão pode ser feita seguindo os passos escritos abaixo:
- Passo 1: Divida o número decimal por 8, anote o resto e atribua-lhe o valor R1. Da mesma forma, anote o quociente e atribua-lhe o valor Q1.
- Passo2: Agora divida Q1 com 8, anote o restante e o quociente. Atribua o valor R2 e Q2 ao restante e ao quociente obtido neste passo.
- Passo3: Repita a sequência até obter o valor do quociente (Qn) igual a 0.
- Passo4: O número de octal será algo parecido com isto: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Exemplo: Vamos considerar um número decimal 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Portanto, o equivalente OCTAL de 2181 é:
(2181) Decimal = (4205) Octal
Conversão de Octal em Sistema de Números Binários:
Novamente, a conversão de octal em decimal é muito semelhante à conversão de binário em decimal, a única diferença é que desta vez vamos multiplicar os dígitos com as potências de 8 em vez de 2. A conversão pode ser feita seguindo os passos escritos abaixo:
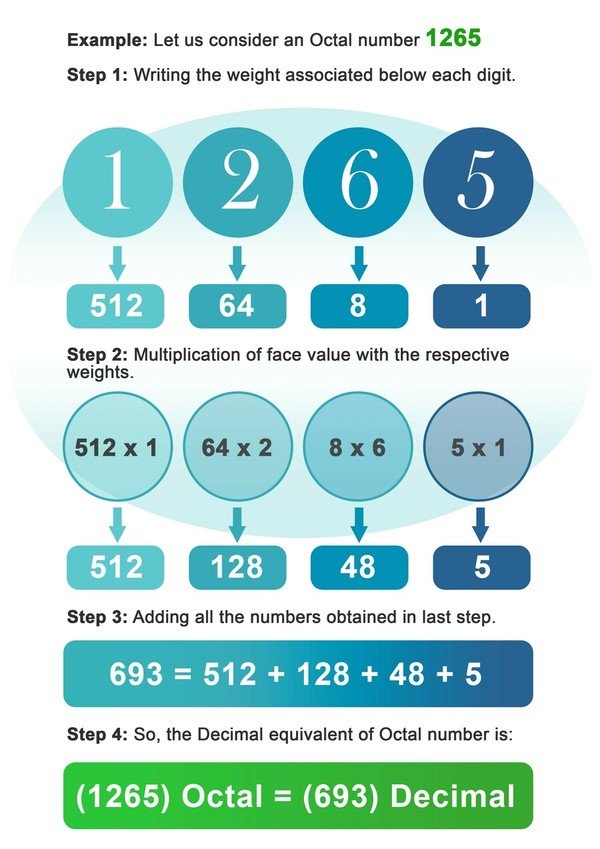
- Passo 1: Escreva o peso de 8 associado abaixo de cada dígito do número octal.
- Passo2: Agora multiplique cada dígito com o peso associado àquele lugar ou índice de dígitos.
- Passo3: Adicione todos os números obtidos após a multiplicação no passo anterior.
- Passo4: O número obtido no último passo é o equivalente decimal do número octal.
Exemplo: Vamos considerar um Octal número 1265.