كيفية التحويل بين نظامي الأعداد الثمانية والعشرية؟
قبل الدخول في حديث تحويل نظام رقمي إلى آخر، دعنا نتحدث قليلا عن نظام الأعداد نفسه. يمكن تعريف نظام الأعداد على أنه مجموعة من تركيبات الرموز المختلفة، حيث يمتلك كل رمز وزنًا محددًا. يتم تمييز أي نظام رقمي بناءً على الأساس الأسي الذي يتم بناء نظام الأعداد عليه. يحدد الأساس الإجمالي لـ "الرقم الأسي" أو "الأساس" عدد الرموز المختلفة المستخدمة في نظام الأعداد المحدد. على سبيل المثال، الأساس لنظام الأعداد الثنائي هو 2، والأساس لنظام الأعداد العشري هو 10، والأساس لنظام الأعداد الثماني هو 8.
نظام الأعداد الثمانية:
وكما يشير الاسم بوضوح، فإن هذا النظام العددي يعتمد على قاعدة تعادل 8. لذلك، لدينا ثمانية أرقام متميزة في هذا النظام العددي. للسهولة، نعتبر هذه الأرقام الثمانية كالأرقام الثمانية الأولى في نظام الأعداد العشرية. ترتبط موقع كل خانة في النظام الثماني بعدد مرتبط بالقوة الثمانية، وتكون هذه القوة مساوية لموضع الخانة من اليسار. يستغرق الأمر ثلاثة أرقام ثنائية كحد أقصى لتمثيل رقم ثماني واحد في الشكل الثنائي. بما أن الأساس لهذا النظام العددي هو قوة بعدد طبيعي، فإنه سهل جدًا وملائم لتحويل الأعداد الثمانية إلى نظام الأعداد الثنائية أو السادس عشري، وهما الأنظمة المستخدمة في الحواسيب لأداء جميع العمليات.
أرقام الأوكتال لا تجد تطبيقًا مباشرًا في آلات الكمبيوتر لأن الكمبيوترات تعمل بنظام ثنائي أو بتات. ومع ذلك، بما أن الرقم الأوكتالي يحتل عددًا أقل من الأرقام ليتم تمثيله في النظام الثنائي، فيمكن تخزينه بكفاءة في الكمبيوتر دون أن يتم إضاعة أي مساحة فارغة في الذاكرة مثل رقم BCD (العشري المشفر ثنائيًا).
تحويل الأنظمة العشرية إلى النظام الثماني:
تحويل العدد العشري إلى ثماني يشبه إلى حدٍ كبير تحويله إلى نظام العد الثنائي. الاختلاف الوحيد هو أننا هذه المرة سنقسم العدد العشري على 8 بدلاً من 2. يمكن إتمام التحويل باتباع الخطوات التالية:
- الخطوة 1: قسم العدد العشري على 8 ، ولاحظ الباقي وقم بتعيين القيمة R1 له. بالمثل ، لاحظ الناتج وقم بتعيين القيمة Q1 له.
- الخطوة 2: الآن قسّم قيمة Q1 على 8، احفظ الباقي والناتج. قم بتعيين القيمة R2 كباقي و Q2 كناتج القسمة المحصلة في هذه الخطوة.
- الخطوة 3: كرر السلسلة حتى تحصل على قيمة الناتج (Qn) تساوي 0.
- الخطوة 4: ستبدو الرقم الثماني مثل هذا: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
لنأخذ في الاعتبار رقمًا عشريًا 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
إذاً، المكافئ الثماني للرقم 2181 هو:
(2181) Decimal = (4205) Octal
تحويل الأعداد الثمانية إلى نظام الأعداد الثنائية.
مجددًا ، تحويل العدد الثماني إلى عشري مشابه جدًا لتحويل العدد الثنائي إلى عشري ، الفرق الوحيد هو أنه في هذه المرة سنقوم بضرب الأرقام بأقواس الثمانية بدلاً من 2. يمكن إجراء التحويل عن طريق اتباع الخطوات المكتوبة أدناه:
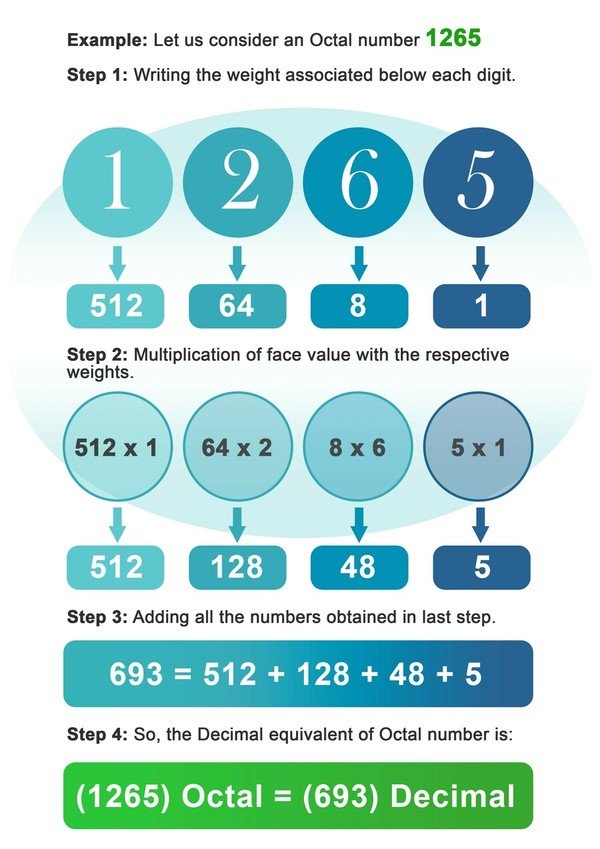
- الخطوة 1: قم بتدوين وزن الأرقام المرتبطة بالرقم الثماني 8 أسفل كل رقم في الرقم الثماني.
- الخطوة 2: الآن ضرب كل رقم بالوزن المرتبط به في تلك المكانة أو الفهرس من الرقم.
- الخطوة 3: أضف جميع الأرقام المحصلة بعد الضرب في الخطوة السابقة.
- الخطوة 4: الرقم الذي تم الحصول عليه في الخطوة السابقة هو المعادل العشري للعدد الثماني.
مثال: لنفترض عددًا ثمانيًا 1265.