¿Cómo convertir entre los sistemas de números octales y decimales?
Antes de entrar en la conversación de conversión de un sistema de números en otro, hablemos un poco del propio sistema de números. El Sistema Numérico puede definirse como el conjunto de las diferentes combinaciones de símbolos, teniendo cada símbolo un peso específico. Cualquier Sistema Numérico se diferencia en base al radix o la base sobre la que está hecho el sistema numérico. El radix o la base define el no total de los diferentes símbolos, que se utiliza en un sistema numérico determinado. Por ejemplo, el radix del sistema numérico binario es 2, el radix del sistema numérico decimal es 10 y el radix del sistema numérico octal es 8.
El Sistema de Número Octal:
Como su nombre lo indica claramente, este sistema numérico se basa en un radix igual a 8. Así que, en este sistema numérico tenemos ocho dígitos distintos. Para facilitar la tarea, consideramos que estos ocho dígitos son iguales a los primeros ocho dígitos del sistema numérico decimal. La posición de cada dígito octal está asociada a una potencia de 8 y esta potencia es igual al índice del dígito de la posición izquierda. Se necesitan como máximo tres dígitos binarios para representar un número octal en forma binaria. Como la base de este sistema numérico en sí mismo es una potencia de dos, es muy fácil y conveniente interconectar un número octal en un sistema numérico binario o hexadecimal que se utiliza en las computadoras para hacer todo el trabajo.
Los números octales no encuentran aplicación directa en la maquinaria de la computadora porque las computadoras trabajan en estados binarios o bits. Sin embargo, como los números octales ocupan menos dígitos para ser representados en binario, pueden ser almacenados eficientemente en la computadora sin que se desperdicie espacio en la memoria como el número BCD (Binary Coded Decimal).
Conversión del sistema de números decimales a octales:
La conversión de decimal a octal es muy similar a la conversión de decimal a binario. La única diferencia es que esta vez dividiremos el número decimal con 8 en lugar de 2. La conversión se puede hacer siguiendo los siguientes pasos escritos:
- Paso 1: Dividir el número decimal por 8, anotar el resto y asignarle el valor R1. De manera similar, anote el cociente y asígnele el valor Q1.
- Paso 2: Ahora divide Q1 con 8, anota el resto y el cociente. Asigne el valor R2 y Q2 al resto y al cociente obtenido en este paso.
- Paso 3: Repita la secuencia hasta obtener el valor del cociente (Qn) igual a 0.
- Paso 4: El número octal se verá algo como esto: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Ejemplo: Consideremos un número decimal 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Así que el equivalente en OCTAL de 2181 es:
(2181) Decimal = (4205) Octal
Conversión de Octal en Sistema Numérico Binario:
De nuevo, la conversión de octal a decimal es muy similar a la conversión de binario a decimal, la única diferencia es que esta vez multiplicaremos los dígitos con las potencias de 8 en lugar de 2. La conversión puede hacerse siguiendo los siguientes pasos escritos:
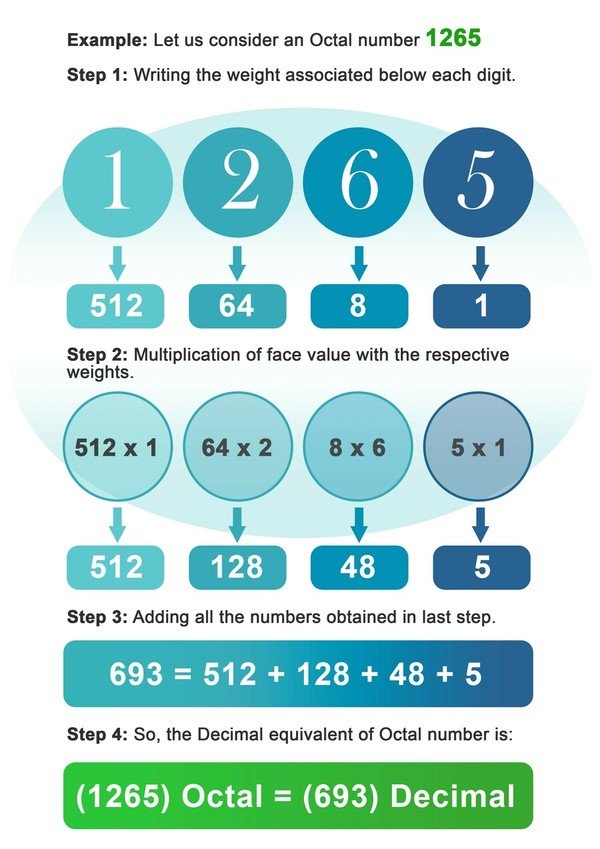
- Paso 1: Escriba el peso de 8 asociado debajo de cada dígito del número octal.
- Paso 2: Ahora multiplica cada dígito con el peso asociado en ese lugar o índice de dígito.
- Paso 3: Sume todos los números obtenidos después de la multiplicación en el paso anterior.
- Paso 4: El número obtenido en el último paso es el equivalente decimal del número octal.
Ejemplo: Consideremos un número octal 1265.