Kā konvertēt astoņciparu un decimālo skaitļu sistēmu?
Pirms sākam sarunu par vienas skaitļu sistēmas pārveidošanu citā, nedaudz parunāsim par pašu skaitļu sistēmu. Skaitļu sistēmu var definēt kā dažādu simbolu kombināciju kopumu, kur katram simbolam ir noteikts svars. Jebkura skaitļu sistēma tiek diferencēta, pamatojoties uz radiksu jeb bāzi, uz kuras šī skaitļu sistēma ir izveidota. Radikss vai bāze nosaka dažādu simbolu kopskaitu, kas tiek izmantots konkrētajā skaitļu sistēmā. Piemēram, bināro skaitļu sistēmas radikss ir 2, decimālskaitļu sistēmas radikss ir 10, bet oktaļu skaitļu sistēmas radikss ir 8.
Astoņskaitļu sistēma:
Kā skaidri norāda nosaukums, šīs skaitļu sistēmas pamatā ir radikss, kas vienāds ar 8. Tātad šajā skaitļu sistēmā ir astoņi dažādi cipari. Vienkāršības labad šos astoņus ciparus uzskatām par tādiem pašiem kā pirmos astoņus ciparus decimālskaitļu sistēmā. Katra astotnieka cipara pozīcija ir saistīta ar kādu 8 pakāpi, un šī pakāpe ir vienāda ar cipara indeksu no kreisās pozīcijas. Viena astoņciparu skaitļa attēlošanai binārajā formā nepieciešami ne vairāk kā trīs bināri cipari. Tā kā šīs skaitļu sistēmas bāze pati par sevi ir kāds divkāršības lielums, ir ļoti viegli un ērti pārveidot astotdaļskaitli binārajā vai heksadecimālajā skaitļu sistēmā, ko izmanto datoros, lai veiktu visus darbus.
Astoņciparu skaitļiem nav tieša pielietojuma datortehnikā, jo datori darbojas ar binārajiem stāvokļiem jeb bitiem. Tomēr, tā kā astoņciparu skaitļi aizņem mazāk ciparu, lai tos attēlotu binārajā sistēmā, tos var efektīvi uzglabāt datorā, netērējot atmiņā tikpat daudz vietas kā BCD (Binary Coded Decimal) skaitļus.
Decimālās skaitļu sistēmas konvertēšana uz oktālo skaitļu sistēmu:
Decimālā skaitļa pārvēršana astoņciparu sistēmā ir ļoti līdzīga decimālā skaitļa pārvēršanai binārajā sistēmā. Vienīgā atšķirība ir tāda, ka šoreiz mēs dalīsim decimālo skaitli ar 8, nevis 2. Pārvēršanu var veikt, sekojot tālāk rakstītajiem soļiem:
- 1. solis: daliet decimālskaitli ar 8, atzīmējiet atlikumu un piešķiriet tam vērtību R1. Līdzīgi, atzīmējiet kvantientu un piešķiriet tam vērtību Q1.
- 2. solis: Tagad daliet Q1 ar 8, atzīmējiet atlikumu un kvantientu. Šajā solī iegūtajam atlikumam un kvantientam piešķir vērtību R2 un Q2.
- 3. solis: Atkārtojiet secību, līdz iegūstat kvantienta (Qn) vērtību, kas vienāda ar 0.
- 4. solis: Astoņskaitlis izskatīsies apmēram šādi.: Rn R(n-1) R(n-2) ……………………... R3 R2 R1
Piemērs: Apskatīsim decimālskaitli 2181.
- 2181 / 8 = ( 272 x 8 ) + 5 ………………………………………... R1 = 5 Q1 = 272
- 272 / 8 = ( 34 x 8 ) + 0 ……………………………………….. R2 = 0 Q2 = 34
- 34 / 8 = ( 4 x 8 ) + 2 ………………………………………... R3 = 2 Q3 = 4
- 4 / 8 = ( 0 x 8 ) + 4 ………………………………………... R4 = 4 Q4 = 0
Tātad OCTAL ekvivalents 2181 ir:
(2181) Decimal = (4205) Octal
Oktaļu skaitļu sistēmas konvertēšana binārajā skaitļu sistēmā:
Astoņciparu pārveidošana decimālskaitļos atkal ir ļoti līdzīga bināro ciparu pārveidošanai decimālskaitļos, vienīgā atšķirība ir tā, ka šoreiz mēs reizināsim ciparus ar 8 reizinājumiem, nevis 2. Pārveidošanu var veikt, sekojot tālāk aprakstītajiem soļiem:
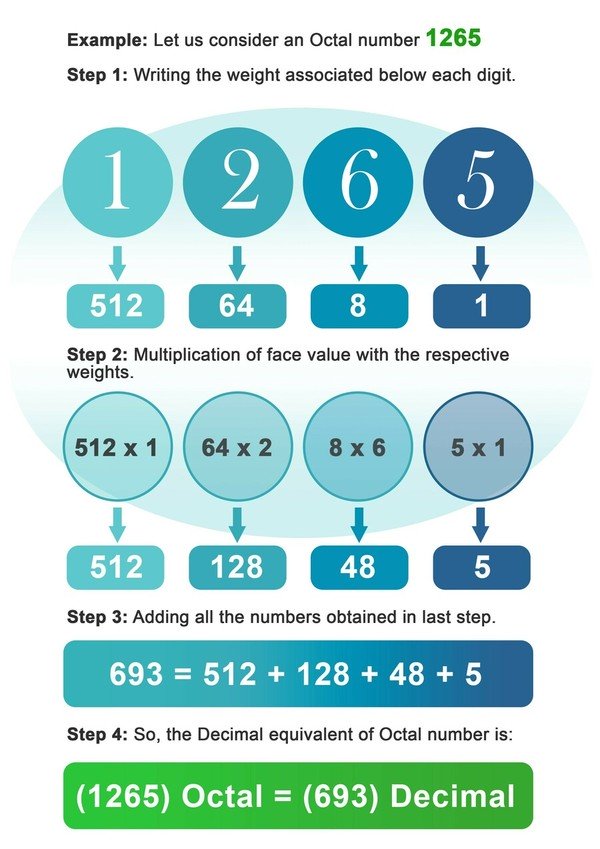
- 1. solis: Ierakstiet zem katra astoņciparu skaitļa cipara saistīto svaru 8.
- 2. solis: Tagad katru ciparu reiziniet ar svaru, kas saistīts ar attiecīgo cipara vietu vai indeksu.
- 3. solis: saskaitiet visus skaitļus, kas iegūti pēc reizināšanas iepriekšējā solī.
- 4. solis: Pēdējā solī iegūtais skaitlis ir astotdaļskaitļa decimālais ekvivalents.
Piemērs: Aplūkosim astoņciparu skaitli 1265.